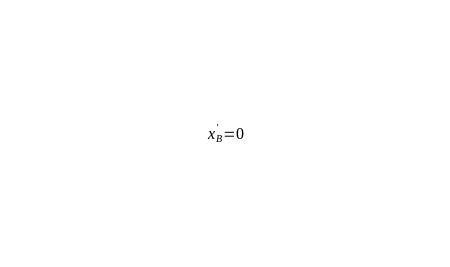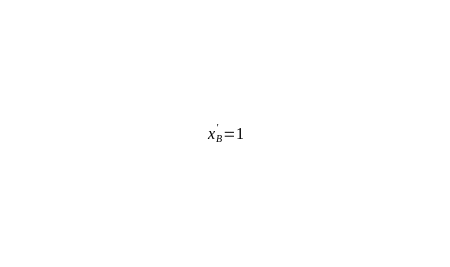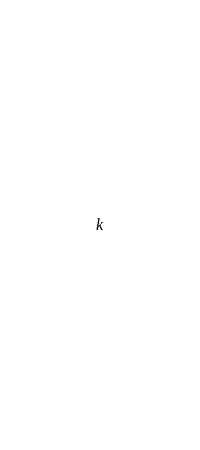～量子計算機による組合せ最適化解法の高精度化を実現～

2025年8月29日
早稲田大学

制約を圧縮して表現する量子技術を開発 ～量子計算機による組合せ最適化解法の高精度化を実現～

詳細は早稲田大学ウェブサイトをご覧ください。

　量子計算機を現実世界の組合せ最適化問題に活用するためには、組合せ最適化問題※1がもつ制約を効率的に取り扱うことが重要となります。これを受け、早稲田大学高等研究所准教授の白井達彦（しらい たつひこ）氏、同大学理工学術院教授の戸川望（とがわ のぞむ）らの研究グループは、組合せ最適化問題がもつ制約を量子計算機で圧縮して表現する技術（図１）を構築し、組合せ最適化の探索効率を向上するための新しい手法を開発しました。さらに本研究グループは、この手法をゲート型量子計算機※2に適用し、実量子計算機を模したシミュレータで精度の改善を確認しました。

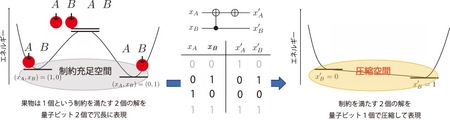
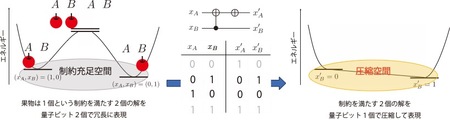
図１　組合せ最適化問題のもつ制約を量子計算機で圧縮して表現するための手法の概要。

図1の補足：図中央上は量子回路を表し、量子ゲート※3（左から制御NOTゲートとXゲート）を作用させることで、表（図中央下）で示した変換を実行する。

キーワード：

組合せ最適化、制約、量子アルゴリズム、圧縮、量子ソフトウェア

（１）これまでの研究で分かっていたこと

　現実世界のあらゆるところに存在する組合せ最適化問題は大規模になるほど、従来型のコンピュータで最適解を得ることが困難になるため、様々な解法が研究されています。中でも近年、ゲート型量子計算機といった量子力学の原理にしたがって動作する新しいタイプの計算機が注目されています。量子計算機は国内外で研究開発され、一般のユーザーもクラウド上で使用できる段階になっています。

　しかし、量子計算機を活用するにはまだ課題が多くあります。とくに制約をもつ組合せ最適化問題を解くことは社会的に重要である一方で、現在の量子計算機では十分な精度を達成することは難しいという課題があります。これまで、この困難を克服するためさまざまな手法が開発されてきました。しかし、これらの手法は、特定のタイプの制約に適用範囲が制限されており、社会課題に現れる複雑な制約をもつ組合せ最適化問題を解くことは依然として困難です。

（２）新たに実現しようとしたこと、明らかになったこと

　今回の研究では、現実世界の組合せ最適化問題に現れる制約に対して汎用的に適用可能な手法を実現しようと試みました。そこで、探索の効率化を実現するため、制約を満たす解の集合を圧縮して表現することを考えました。たとえば、図１では、１個の果物をAlice（以下A）とBob（以下B）のどちらかに与えるという問題を考えます。それぞれAとBに１個ずつの量子ビットを対応させ、量子ビットが１のとき果物を与える、量子ビットが0のとき果物を与えないとします。すると２個の量子ビットが必要となります。このとき、果物の個数は１個ですので、２個の量子ビットのうち、一方は０、もう一方は１とする必要があります。これが制約です。ところが量子計算機は一般に制約を満たさない解を出力します。たとえば、２個の量子ビットの両方が０あるいは両方が１となるような解です。このような制約を満たさない解があるとエネルギー地形が複雑化（凸凹）するため、量子アルゴリズムの精度を悪化させる要因となります。そこで、制約を満たす解の個数が２個であることに着目し、１個の量子ビットでこれらを表現することを考えます。具体的には、図１の表で与えられる変換を考えます。このとき、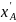 を０に固定した解空間を考える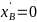と、 と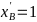 がそれぞれ制約を満たす解に対応しています。このように、もともと２個の量子ビットで表現されていた制約を満たす解空間を１個の量子ビットで圧縮して表現できることがわかります。こうしたもともとの問題で必要とする量子ビットの個数より、少ない個数の量子ビットで表現された空間を圧縮空間と呼びます。圧縮空間では探索する必要のある解の個数が減るため、精度高く最適解を探索できることが期待されます。

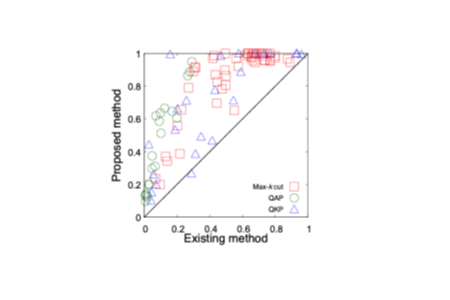
　今回の研究では、ゲート型量子計算機を用いて圧縮空間を構築する方法を明らかにしました。圧縮空間を与える変換は、ゲート型量子計算機で操作する量子ゲートを組み合わせて表すことができます。そこで、組合せ最適化問題の制約に応じて、圧縮空間を構成する量子ゲートの組合せを探索するための量子アルゴリズムを開発しました。この方法は、原理的にはあらゆるタイプの制約に適用でき、現実世界に現れる多くの組合せ最適化問題に対して有効です。さらに典型的な制約をもつ組合せ最適化問題に対して、具体的に本手法が適用可能であることを示しました。実際に、量子計算機で解くことが困難とされる３つのタイプの組合せ最適化問題に対して、本手法を組み込んだ場合（提案手法）と組み込まなかった場合（従来手法）とを比較した結果、提案手法で得られた答えの精度が高いことがわかりました（図２）。

図2．手法の比較

図2の補足：縦軸横軸の値は各組合せ最適化問題の最適解が得られる確率を表しています（1が最も精度が高い）。縦軸に提案手法、横軸に従来手法を示しました。四角（赤色）のデータは最大kカット問題※4（k=3,4 ）、丸（緑色）のデータは二次ナップサック問題※5、三角（青色）のデータは二次割当問題※6を表し、それぞれシミュレータを用いて実験を行った結果をプロットしています。データが対角線の上側にあることは、提案手法において従来手法より性能が改善していることを示しています。

（３）研究の波及効果や社会的影響

　本手法を使うことによって、より精度高くさまざまな制約をもつ組合せ最適化問題を解くことができます。本手法は量子計算機に簡単に導入することができることから、現在のまた近未来的に実現する量子計算機の性能を最大限引き出すための量子ソフトウェア開発の要素技術として利用されることが期待されます。たとえば、今回の手法により交通流の最適化が実現すると、渋滞の解消や二酸化炭素排出量の削減など社会的問題へ大きく貢献する可能性があります。

（４）課題、今後の展望

　本手法では、組合せ最適化問題のもつ制約を量子計算機で圧縮して表現する手法を開発しました。今後、量子計算機の性能が向上するとともに、一層広範囲の組合せ最適化問題に適用可能となることが期待されます。また、圧縮空間を構築する方法は、組合せ最適化問題にとどまらず、化学計算や機械学習などへの応用が考えられます。実世界に見られるさまざまな具体的な問題に対して、本手法の有効性を検証していきます。

（５）研究者のコメント

　本研究ではゲート型量子計算機を精度高く利用するための手法を開発しました。本研究で開発した手法を使うことで、量子計算機の性能が最大限発揮され、今後新たに量子計算機を活用できる事例が増えることを期待します。

（６）用語解説

※１　組合せ最適化問題

膨大な選択肢の中から､与えられた制約を満たしつつ、関数の最小値（または最大値）をとる選択肢を求める問題の総称。

※2　ゲート型量子計算機

現在の計算機を構成するビットを量子ビットで置き換えた計算機であり、量子ゲートと呼ばれる演算を量子ビットに作用させることで動作する。

※3　量子ゲート

ゲート型量子計算機における演算素子。図１で示した、制御NOTゲートとXゲートは、古典計算における排他的論理和やNOTに対応する。

※4　最大kカット問題

与えられたグラフの頂点集合を、異なる部分集合間を繋ぐ辺の数を最大にするようにk個の部分集合に分割する組合せ最適化問題。

※5　二次ナップサック問題

ナップサックの容量と品物の価値が与えられたとき、容量を超えない範囲でナップサックに入れる品物の総価値を最大化する組合せ最適化問題。

※6　二次割当問題

工場と地点が同じ個数与えられたとき、各工場を各地点に割り当てたときの地点間の輸送コストの合計を最小化する組合せ最適化問題。

（７）論文情報

雑誌名：IEEE Transactions on Quantum Engineering

論文名：Compressed space quantum approximate optimization algorithm for constrained combinatorial optimization

執筆者名（所属機関名）：Tatsuhiko Shirai*（早稲田大学）、 Nozomu Togawa（早稲田大学）

掲載予定日時：2025年8月25日

掲載URL：https://ieeexplore.ieee.org/document/11139119

DOI：https://doi.org/10.1109/TQE.2025.3602404

*：責任著者

（８）研究委託

研究委託元：NEDO（国立研究開発法人新エネルギー・産業技術総合開発機構）

研究課題名：JPNP16007「高効率・高速処理を可能とするAIチップ・次世代コンピューティングの技術開発／次世代コンピューティング技術の開発／量子計算及びイジング計算システムの総合型研究開発」

代表機関：国立研究開発法人産業技術総合研究所

本学の研究代表者名：戸川望（早稲田大学）

（９）研究助成

研究費名：科研費・若手研究

研究課題名：23K13034「非平衡量子開放系における物性制御法の開発」

研究代表者名：白井達彦（早稲田大学）